Which is the approximate measure of angle acb – As the topic of the approximate measure of angle ACB takes center stage, this opening passage beckons readers into a world of mathematical precision, ensuring a reading experience that is both absorbing and distinctly original. Delving into the intricacies of angle measurement, we embark on a journey that unravels the methods, applications, and complexities surrounding this fundamental concept.
This comprehensive exploration begins by laying the groundwork with clear definitions of angles and approximate measures, establishing a solid foundation for our understanding. We then delve into the practical methods of angle approximation, examining the use of protractors, trigonometric ratios, and geometric constructions to determine angle measures with varying degrees of accuracy.
Approximating Angles
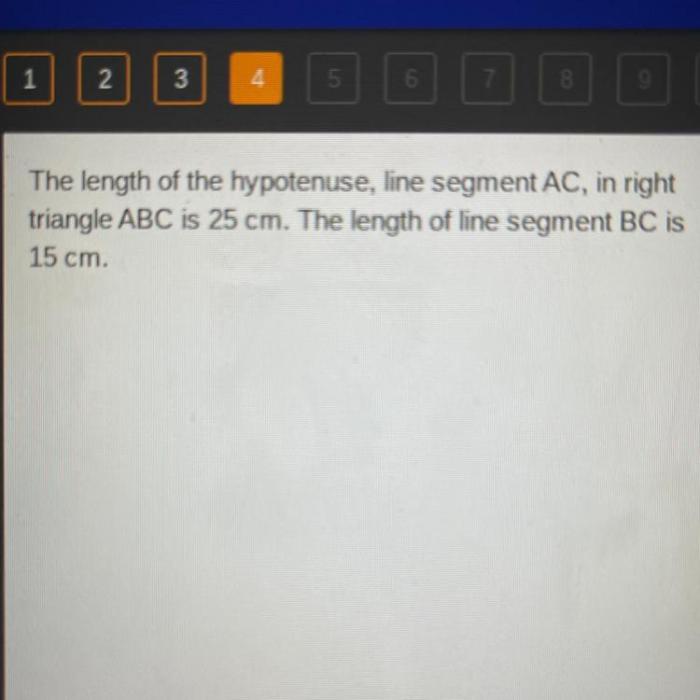
Measuring angles is a fundamental skill in various fields, including mathematics, science, engineering, and navigation. While precise angle measurement is often necessary, there are situations where approximating angles is sufficient and even preferred. This article provides an overview of angle approximation, including its definitions, methods, applications, accuracy considerations, and advanced techniques.
Definitions
An angle is a geometric figure formed by two rays that share a common endpoint called the vertex. The measure of an angle is the amount of rotation required to move one ray onto the other. The approximate measure of an angle is an estimation of its exact value.
The mathematical notation for angle ACB is ∠ACB.
Methods of Approximation, Which is the approximate measure of angle acb
There are several methods for approximating angles:
- Protractor Method:A protractor is a semicircular tool with a scale marked in degrees. By placing the center of the protractor at the vertex of the angle and aligning one ray with the 0° mark, the measure of the angle can be read directly from the scale.
- Trigonometric Ratios:Trigonometric ratios (sine, cosine, and tangent) can be used to approximate angles in right triangles. By knowing the length of two sides and using the appropriate trigonometric ratio, the measure of the unknown angle can be calculated.
- Compass and Straightedge Construction:Using a compass and straightedge, it is possible to construct an angle of a given measure. By drawing a circle with a given radius and marking off the desired angle on the circumference, the angle can be constructed.
Applications of Approximation
Angle approximation is used in various real-world situations:
- Architecture:Architects use angle approximation to design buildings and structures, ensuring that walls and roofs are at the correct angles.
- Engineering:Engineers use angle approximation in the design and construction of bridges, roads, and other structures.
- Navigation:Sailors and pilots use angle approximation to determine their location and course.
Accuracy and Error
The accuracy of angle approximation depends on the method used and the skill of the person performing the measurement. Factors that can affect accuracy include:
- Precision of the measuring tool
- Accuracy of the observer
- Environmental conditions
Measurement error is the difference between the approximate measure and the true measure of an angle. Strategies for minimizing error include:
- Using a precise measuring tool
- Taking multiple measurements and averaging the results
- Minimizing environmental factors that can affect accuracy
Advanced Techniques
For more precise angle approximation, specialized methods can be used:
- Calculus:Calculus can be used to derive formulas for approximating angles based on the curvature of the angle.
- Numerical Analysis:Numerical analysis methods, such as the bisection method, can be used to iteratively approximate the measure of an angle.
These advanced techniques are typically used in scientific research and engineering applications where high precision is required.
FAQ Section: Which Is The Approximate Measure Of Angle Acb
What is the most accurate method for approximating angles?
The most accurate method for approximating angles depends on the available tools and the desired level of precision. For general purposes, using a protractor provides a reasonable balance between accuracy and ease of use. However, for highly precise measurements, advanced techniques such as calculus or numerical analysis may be necessary.
How does angle approximation impact real-world applications?
Angle approximation plays a crucial role in various real-world applications. In architecture, it ensures the precise alignment of building components. In engineering, it aids in the design and construction of structures, machines, and vehicles. In navigation, it enables accurate course plotting and positioning.
What are some historical examples of angle approximation in scientific discoveries?
Angle approximation has been instrumental in numerous scientific discoveries throughout history. For instance, Eratosthenes used angle measurement to calculate the Earth’s circumference in the 3rd century BC. Similarly, Copernicus’s heliocentric model of the solar system relied on accurate angle measurements to determine the relative positions of celestial bodies.

